

Using f\left(x\right) (miles driven) as an input value for g\left(y\right), where gallons of gas depends on miles driven, does make sense. The function g\left(y\right) requires a number of miles as the input. The expression f\left(x\right) takes hours as input and a number of miles driven as the output.

Then click the button and select 'Solve the function operation' to compare your answer to Mathways. Try the entered exercise, or type in your own exercise.
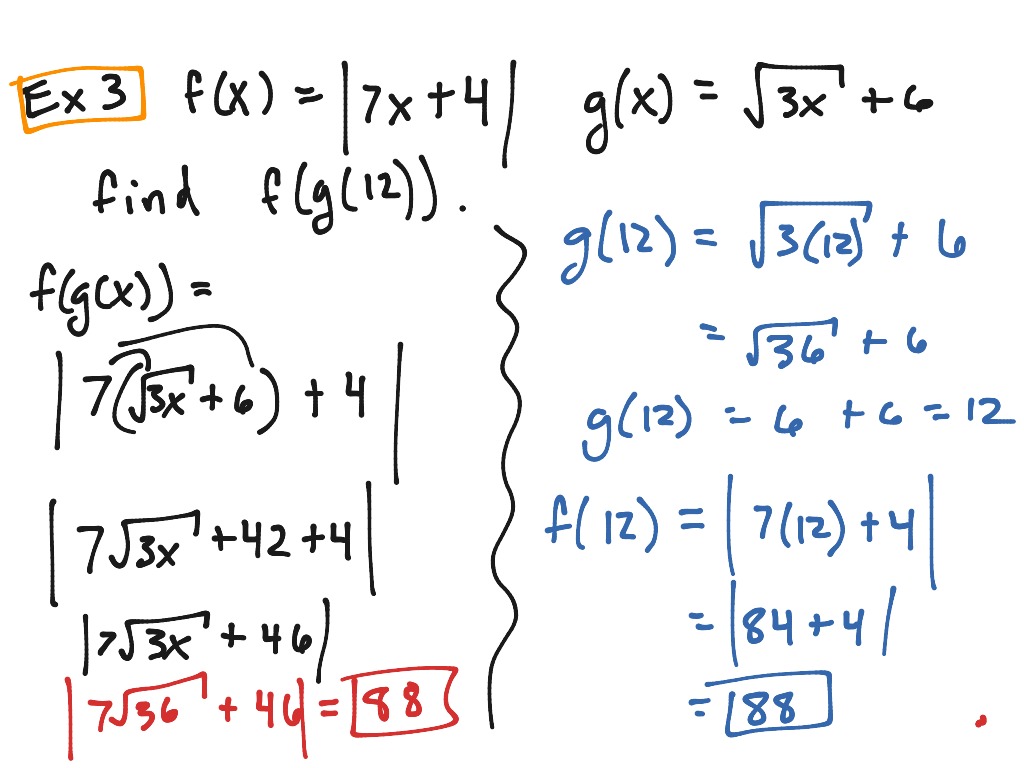
You can use the Mathway widget below to practice function composition. The expression f\left(g\left(y\right)\right) is meaningless. This is fully simplified, so my answer is: ( g g ) ( x) x4 + 10 x2 20.

Trying to input a number of gallons does not make sense. The function f\left(x\right) requires a number of hours as the input. The expression g\left(y\right) takes miles as the input and a number of gallons as the output. In other words in many cases f\left(g\left(x\right)\right)\ne g\left(f\left(x\right)\right) for all x.įor example if f\left(x\right)=\right) In general f\circ g and g\circ f are different functions. Then the function f takes g\left(x\right) as an input and yields an output f\left(g\left(x\right)\right). Another way is to carry out the usual algebraic operations on functions, such as addition, subtraction, multiplication and division. In the equation above, the function g takes the input x first and yields an output g\left(x\right). Function composition is only one way to combine existing functions. We follow the usual convention with parentheses by starting with the innermost parentheses first, and then working to the outside. It is also important to understand the order of operations in evaluating a composite function. However, it is important not to confuse function composition with multiplication because, as we learned above, in most cases f\left(g\left(x\right)\right)\ne f\left(x\right)g\left(x\right). Composition is a binary operation that takes two functions and forms a new function, much as addition or multiplication takes two numbers and gives a new number. We use this operator mainly when we wish to emphasize the relationship between the functions themselves without referring to any particular input value. The open circle symbol \circ is called the composition operator. We read the left-hand side as ``f composed with g at x,'' and the right-hand side as ``f of g of x.'' The two sides of the equation have the same mathematical meaning and are equal. \left(f\circ g\right)\left(x\right)=f\left(g\left(x\right)\right) We represent this combination by the following notation: The resulting function is known as a composite function. The process of combining functions so that the output of one function becomes the input of another is known as a composition of functions. When we wanted to compute a heating cost from a day of the year in the introductory example, we created a new function that takes a day as input and yields a cost as output. Performing algebraic operations on functions combines them into a new function, but we can also create functions by composing functions. Now, enter h(x) = f(x)+g(x) into the next line.Įvaluate h(1), why do you think you get this result? Create a New Function Using a Composition Use an online graphing calculator to graph the following functions: Let’s explore what happens to the graphs of functions that are combined using algebraic operations. If w\left(y\right) is the wife’s income and h\left(y\right) is the husband’s income in year y, and we want T to represent the total income, then we can define a new function. We want to do this for every year, adding only that year’s incomes and then collecting all the data in a new column. Suppose we need to add two columns of numbers that represent a husband and wife’s separate annual incomes over a period of years, with the result being their total household income. We do this by performing the operations with the function outputs, defining the result as the output of our new function. Another way to combine functions is to carry out the usual algebraic operations on functions, such as addition, subtraction, multiplication and division.


 0 kommentar(er)
0 kommentar(er)
